The author of Men of Mathematics, E.T. Bell, wrote about mathematicians that changed our world. This book was written in the late 1930s, shortly after Einstein formulated his theory of general relativity and quantum mechanics was just beginning to be understood. While this book does not require advanced knowledge of mathematics, it is obvious that Bell expected this book to be read by intellectuals with a keen interest in math. He wrote this book to make the world understand the men behind these earth-shattering discoveries. The lives and works of mathematicians could be considered a dry topic by some, but Bell does an effective job of keeping the reader engaged.
This book offers a short synopsis of the lives and discoveries of a multitude of mathematicians, up to 1937. These were some weird dudes. Euler (left) made the most contributions to mathematics in history (and did most of his good stuff when he was blind!). Newton invented calculus because he didn't want to go outside and mingle with intellectual plebs. Lagrange (sort of) figured out a solution to the three body problem, the only question to ever make Newton's head ache.
Euler was a busy dude. He was, in fact, "the most prolific mathematician in history". Some even referred to him as "analysis incarnate". "It has been estimated that sixty to eighty large quarto volume will be required for the publication of his collected works". Euler has yet to be surpassed (as of 2013) as an algorist (one who develops algorithms). And, as previously mentioned, he was blind for the last 17 years of his life. Did this hold him back? No! When he realized he was going blind (for the second time), he taught his son to be a mathematical scribe. Some of Euler's greatest works were done during this time. Euler had a supernatural gift for linking apparently unrelated equations; he loved beautiful formulas for their own sake. Euler's strangest gift to us most definitely lies in the relation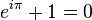 
. Think about that for a second. That is super weird. Euler continued his legacy in his close associate and quasi-student, Lagrange.
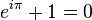. Think about that for a second. That is super weird. Euler continued his legacy in his close associate and quasi-student, Lagrange.
Lagrange was the apple of Napoleon's eye and the protege of Euler. He became a senator, a count of the empire, and a Grand Officer of the Legion of Honor (thanks to Napoleon). Lagrange was strictly against diagrams; the preface of his textbook read "No diagrams will be found in this work". Ironically, he served as a stepping stone for Einstein's theory of general relativity by describing mechanics as the geometry of space of four dimensions (three cartesian coordinates for position and one for time). He tackled the three-body problem (the gravitational interaction between the sun, the earth and the moon), thereby partially solving the only problem that Newton couldn't figure out.
Newton, too, was a busy dude. He invented (yes Ms. Colberg, I said "invented") calculus! His successors point to him "as the supreme intellect that the human race has produced". High praise indeed, but well deserved. He was convinced that light is indeed a particle (kind of) about 400 years before the rest of the world caught up with him. He formulated the universal law of gravitation, and he came up with those famous three laws of motion. Newton's brain changed the world.
This book is about math, but it is not a math textbook. To avoid giving readers death by boredom, Bell peppers the mathematics with short biographical synopses about the men behind the principles. Without this human element, this book would be dull and common. To engage the reader further, Bell occasionally adopts a humorous tone: when explaining that Lagrange felt no connection to his biological mother that left him on the steps of a church as a baby, the author quotes Lagrange as saying "You are only my stepmother", then parenthetically comments "a good pun in English, but not in French", making it clear that Bell is a real person that enjoys a good laugh now and then. Bell also makes sparing but charming use of alliteration ("decisive die") to make the reader sit up and re-engage with the book. Bell uses italics and varied typesetting to the same effect as the aforementioned alliteration (see what I did there?).
To make the mathematics of this book slightly less daunting, the author makes copious use of diagrams and mathematical typesetting. The author explains a concept and later reinforces it algebraically or visually. This helps to break the monotony of reading academic mathematical proofs. While Bell explains how a mathematical concept works, he also explains how the mathematician derived the concept, reminding the reader of the purpose of the book.
This book is well grounded and not self-important. Though the title and the mathematics discussed may sound daunting, the author does a good job of writing so a non-math-major can understand the concepts. Bell is not an elitist, but he does write in such a way that at least a modicum of intelligence and critical thinking is required to fully understand and appreciate his book. Therefore, I give this book a superciliousness factor of 6 (10 being the Principia by dearest Newton, 1 being Beavis and Butthead). If you have an interest in mathematics and would like to learn more about "the lives and achievements of the great mathematicians", I highly recommend that you read this book.
